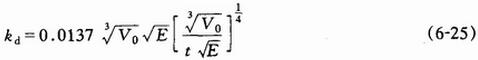闪蒸液体或加压气体瞬时泄漏后,有一段快速扩散时间,假定此过程相当快以致在混合气团和周围环境之间来不及热交换,则此扩散称为绝热扩散。
根据TNO(1979年)提出的绝热扩散模式,泄漏气体(或液体闪蒸形成的蒸气)的气团呈半球形向外扩散。根据浓度分布情况,把半球分成内外两层,内层浓度均匀分布,且具有50%的泄漏量;外层浓度呈高斯分布,具有另外50%的泄漏量。
绝热扩散过程分为两个阶段:第一阶段,气团向外扩散至大气压力,在扩散过程中,气团获得动能,称为“扩散能”;第二阶段,扩散能再将气团向外推,使紊流混合空气进入气团,从而使气团范围扩大。当内层扩散速度降到一定值时,可以认为扩散过程结束。
A 气团扩散能
在气团扩散的第一阶段,扩散的气体(或蒸气)的内能一部分用来增加动能,对周围大气做功。假设该阶段的过程为可逆绝热过程,并且是等熵的。
a 气体泄漏扩散能
根据内能变化得出扩散能计算公式如下:
式中 E——气体扩散能,J;
Cv——定容比热,J/(kg·K);
T1——气团初始温度,K;
T2——气团压力降至大气压力时的温度,K;
p0——环境压力,Pa;
V1——气团初始体积,m3;
V2——气团压力降至大气压力时的体积,m3。
b 闪蒸液体泄漏扩散能
蒸发的蒸气团扩散能可以按下式计算:
式中 E——闪蒸液体扩散能,J;
H1——泄漏液体初始焓,J/kg;
H2——泄漏液体结束时焓,J/kg;
Tb——液体的沸点,K;
S1——液体蒸发前的熵,J/(kg·K);
S2——液体蒸发后的熵,J/(kg·K);
W——液体蒸发量,kg;
p1——初始压力,Pa;
p0——周围环境压力,Pa;
V1——初始体积,m3。
B 气团半径与浓度
在扩散能的推动下气团向外扩散,并与周围空气发生紊流混合。
a 内层半径与浓度
气团内层半径R1和浓度c是时间函数,表达如下:
式中 t——扩散时间,s;
V0——在标准温度、压力下气体体积,m3;
kd——紊流扩散系数,按下式计算:
如上所述,当中心扩散速度(dR/dt)降到一定值时,第二阶段才结束。临界速度的选择是随机的且不稳定的。设扩散结束时扩散速度为1m/s,则在扩散结束时内层半径R1和浓度c可按下式计算:
b 外层半径与浓度
第二阶段末气团外层的大小可根据试验观察得出,即扩散终结时外层气团半径R1由下式求得:
R2=1.456R1 (6—28)
式中 R1,R2——分别为气团内层、外层半径,m。
外层气团浓度自内层向外呈高斯分布。