被测物发射率对红外热像仪测温精度的影响-Telops红外专家教你如何选择红外热像仪之三

本文通过实验探索被测目标发射率与测温精度的关系。

测温实验

本实验使用近距离探测，因而可以忽略大气衰减，把被测物表面看做满足灰体模型，抵达红外探测器的辐射总能量应为被测物红外辐射的能量与目标反射的环境辐射能量之和，以此我们立式1 ：
Ｌｍ＝εＬｔ＋（１－ε）Ｌｂ

式中Ｌｍ为到达镜头前的总辐射亮度，Ｌｔ为目标的辐射亮度，Ｌｂ为环境的辐射亮度，ε为目标表面发射率。因为灰体的反射和发射均是漫反射，所以辐射亮度Ｌ与辐射出射度Ｍ存在如下关系，式2 ：Ｌ＝Ｍ π，

由普朗克辐射定律，立式：

Ｍｔ＝∫ ^１４ _８ｄλ(ｃ１λ^－５)／(ｅ^{ｃ２／λＴｔ} －１) ，（３）

Ｍｂ＝∫ ^１４ _８ｄλ(ｃ１λ^－５) ／(ｅ^{ｃ２／λＴｔ} －１ )，（４）式中Ｍｔ为目标的辐射出射度，Ｍｂ为环境的辐射出射度，Ｔｔ为目标0K，Ｔｂ为环境0K，λ为波长，ｃ１为第一辐射常数（３７４１８×１０－１６Ｗ· ｍ２），ｃ２为第二辐射常数（１４３８８×１０－２ｍ·Ｋ）。

将式（２）、（３）、（４）代入式（１）得：

Ｌｍ＝ ε /π∫ ^１４ _８ｄλ(ｃ_１λ^－５ )/(ｅ^{ｃ２／λＴｔ} －１ )＋１－ε π ∫ ^１４ _８ｄλ(ｃ１λ^－５ )/(ｅ^{ｃ２／λＴｂ} －１ )．（５）红外热像仪根据设置的目标表面发射率和采集的环境温度，结合测得的辐射亮度，由式（５）得出目标的温度。

由普朗克辐射定律，可以认为Ｌｔ是Ｔｔ为自变量的函数，记作：

Ｌ_ｔ_＝ｆ（Ｔ_ｔ_{）＝ (１/π)∫ ^１４}_８ｄλ(ｃ１λ^－５ )/(ｅ^{ｃ２／λＴｂ} －１ )．（６）则有：Ｔ_ｔ＝ｆ^－１（Ｌｔ）．（７）为便于分析和数值计算，将影响红外热像仪测温精度的因素用差分形式表示：

_{ΔＴｔ＝ｆ－１（Ｌｔ＋ΔＬｔ）－ｆ－１（Ｌｔ），（８）}

_{由式（１）可得： ΔＬｔ＝[(Ｌｂ－Ｌｍ )/ε２ ]·Δε－ ΔＬｂ(１－ε)/ ε，（９）}

_{其中： ΔＬｂ＝ｆ（Ｔｂ＋ΔＴｂ）－ｆ（Ｔｂ），（１０）}

_{根据式（８）、（９）、（１０），可以计算红外热像仪测温误差。}

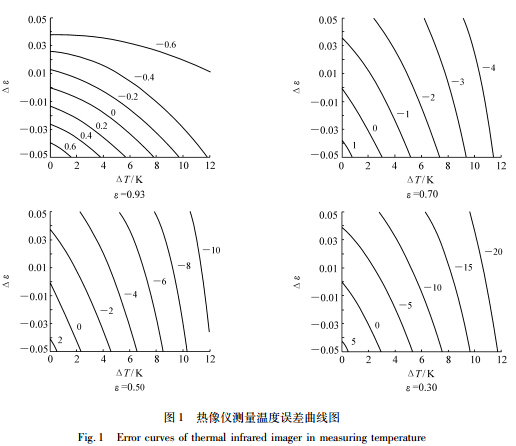从上述分析可以看到，红外热像仪的测温误差ΔＴｔ取决于 Δε、ε、ΔＴｂ、Ｔｂ和Ｌｍ。为了表现出目标表面发射率对红外热像仪测温精度的影响,本实验假定环境温度293.15K,目标温度308.15K,对被测目标表面发射率为0.95、0.7、0.5、0.3时分别进行理论计算，其结果如右图所示。

分析右图可知，被测物发射率对红外热像仪测温精度具有一定的影响。一般来说目标表面发射率越小，测温误差越大；目标表面发射率越大，测温误差越小。所以高精度的红外热像仪必须能够手动或者自动设定被测目标的发射率。

根据以上分析，红外热像仪应当避免测量目标表面发射率很小的目标温度。

Telops对被测物发射率所做的努力是，在红外热像仪配套软件中手动调整被测目标（灰体）的发射率，软件会自动根据灰体设置的发射率对测温数据进行校正。